Publicado originalmente el 18 Octubre 2014

Patronaje de la crinolina 2
Este post es en realidad la continuación del post anterior: Patronaje de la crinolina.
En este post hablaremos de cómo poder calcular a que distancia se encuentran las varillas sin tener que trazar los arcos, procedimiento que dimos en el post anterior. Es interesante para los que realicen patronaje por ordenador sea con programas de dibujo vectorial o con aplicativos directamente desarrollados para el patronaje. Un simple cálculo nos evita de trazar dos arcos y buscar la línea tangente a ambos arcos.
Para hallar la altura que separa dos líneas de varillas ( o la cintura con la primera línea de varillas) utilizaremos el teorema de Pitágoras después de haber reducido el volumen de un trapecio regular en los volómentes de un rectángulo y de dos triángulos rectángulos .
Para conocer la distancia que separa dos varillas deberemos hacer un cálculo para cada dos varillas.
En la siguiente imagen muestro el resultado del trazado entre la cintura y la primera varilla.
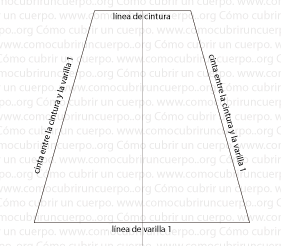
Vemos que el resultado del trazado es un trapecio recular en el que tenemos las siguientes variables
lc= línea de cintura
lv= línea de varilla 1
ccv= cinta entre la cintura y la varilla 1
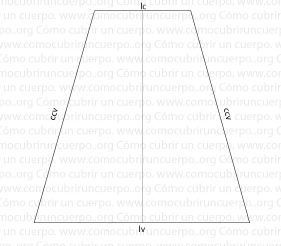
Si trazamos dos perpendiculares a la línea más larga (lv) que acaben en el vértice de la lc con la línea ccv obtendremos la siguiente imagen. Las nuevas líneas las llamaremos h
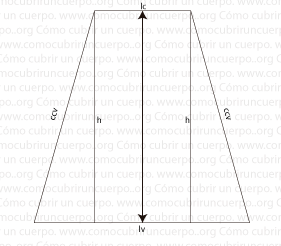
Si nos fijamos bien hemos descompuesto el trapecio regular en dos triángulos rectángulos y en rectángulos. Los dos triángulos rectángulos son evidentemente iguales.
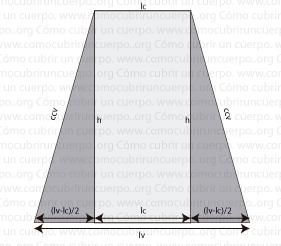
En la parte interior de la imagen hemos descompuesto el recorrido Lv.
Lv es igual a lc + (lv-lc) , el excedente (lv-lc) está repartido en dos partes iguales cada una a un lado de lv por lo que cada lado será (lv-lc)/2.
Ahora si nos fijamos en uno de los dos triángulos rectángulos veremos que uno de los dos catetos es la distancia (lv-lc)/2, el otro cateto (h), es el que buscamos y que sy hipotenusa es la distancia ccv.
Sabemos que la hipotenusa al cuadrado de un triángulo rectángulo es igual a la suma de los dos cateos al cuadrado, por lo que el valor h será igual a la raíz cuadrada de ccv al cuadrado menos (lv-lc)/2 al cuadrado.
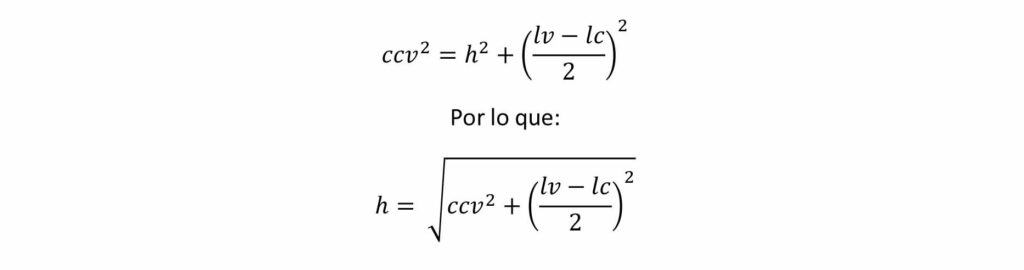
Una vez hallado este valor procederemos análogamente con la siguiente distancia entre las sucesivas varillas.
